三角形的四心的向量表示-白红宇

三角形的四心的向量表示

阅读量：6999 次

发布时间：2019-06-27

本文共 5560 字，大约阅读时间需要 18 分钟。

前言

一、三角形重心

重心：三角形的三条中线的交点。

命题一、已知$O$为$\Delta ABC$内的一点，若$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\vec{0}$，则$O$是$\Delta ABC$的重心；

证明：必要性，由于$O$是$\Delta ABC$的重心，则线段$AD、BE、CF$为三角形的三条中线，

则有$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}=\cfrac{4}{3}\overrightarrow{AO}=-\cfrac{4}{3}\overrightarrow{OA}$，

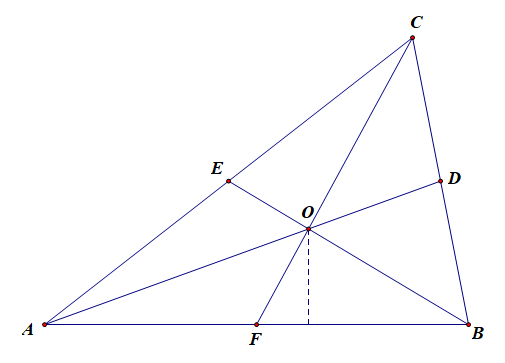
$\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BE}=\cfrac{4}{3}\overrightarrow{BO}=-\cfrac{4}{3}\overrightarrow{OB}$，

$\overrightarrow{CB}+\overrightarrow{CA}=2\overrightarrow{CF}=\cfrac{4}{3}\overrightarrow{CO}=-\cfrac{4}{3}\overrightarrow{OC}$，

故$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$

$=-\cfrac{4}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})$

$=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{CB}+\overrightarrow{CA}=\vec{0}$；

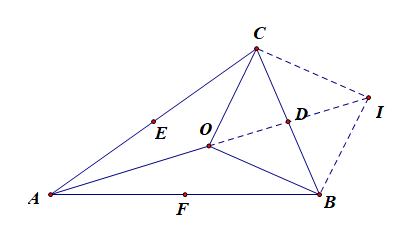
充分性，由$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\vec{0}$，

得到$\overrightarrow{OB}+\overrightarrow{OC}=-\overrightarrow{OA}$，

又$\overrightarrow{OB}+\overrightarrow{OC}=2\overrightarrow{OD}$，

则$-\overrightarrow{OA}=2\overrightarrow{OD}$，

故点$A、O、D$三点共线，且$AD$为三角形的一条中线；

同理，$BE、CF$为三角形的中线；故$O$是$\Delta ABC$的重心；证毕。

命题二、$O$是$\Delta ABC$的重心，则$S_{\Delta AOB}=S_{\Delta BOC}=S_{\Delta COA}$；

证明：$O$是$\Delta ABC$的重心，令边$AB$上的高线为$h$，

则$S_{\Delta AOB}=\cfrac{1}{2}\cdot AB\cdot \cfrac{h}{3}=\cfrac{1}{3}S_{\Delta ABC}$，

同理，$S_{\Delta BOC}=\cfrac{1}{3}S_{\Delta ABC}$，

$S_{\Delta AOC}=\cfrac{1}{3}S_{\Delta ABC}$，

故$S_{\Delta AOB}=S_{\Delta BOC}=S_{\Delta COA}$；

命题三、已知$D、E、F$是$\Delta ABC$的边$BC、AC、AB$的中点，则$\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\vec{0}$；

证明：已知$D、E、F$是$\Delta ABC$的边$BC、AC、AB$的中点，$O$是$\Delta ABC$的重心，

则$\overrightarrow{AD}=\cfrac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$，

$\overrightarrow{BE}=\cfrac{1}{2}(\overrightarrow{BC}+\overrightarrow{BA})$，

$\overrightarrow{CF}=\cfrac{1}{2}(\overrightarrow{CA}+\overrightarrow{CB})$，

故$\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}$

$=\cfrac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BC}+\overrightarrow{BA}+\overrightarrow{CA}+\overrightarrow{CB}) =\vec{0}$；

命题四、平行四边形$ABCD$的中心是$O$，$P$为平面上任意一点，则$\overrightarrow{PO}=\cfrac{1}{4}(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD})$；

证明：平行四边形$ABCD$的中心是$O$，$P$为平面上任意一点，

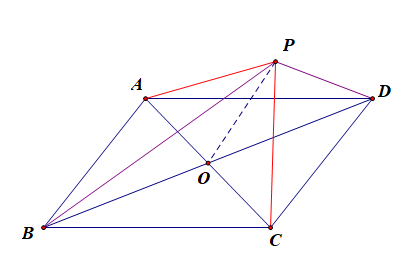
则在$\Delta PAC$中，$\overrightarrow{PA}+\overrightarrow{PC}=2\overrightarrow{PO}$，

在$\Delta PBD$中，$\overrightarrow{PB}+\overrightarrow{PD}=2\overrightarrow{PO}$，

故$\overrightarrow{PA}+\overrightarrow{PC}+\overrightarrow{PB}+\overrightarrow{PD}$

$=4\overrightarrow{PO}$，

即$\overrightarrow{PO}=\cfrac{1}{4}(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD})$；

二、三角形外心

外心：三角形的三条边的中垂线交点，外接圆的圆心

已知$O$为$\Delta ABC$内的一点，满足$|\overrightarrow{OA}|=|\overrightarrow{OB}|=|\overrightarrow{OC}|$，则$O$是$\Delta ABC$的外心；

三、三角形垂心

垂心：三角形的三条边的高线的交点。

命题一、已知$O$为$\Delta ABC$内的一点，满足$\overrightarrow{OA}\cdot\overrightarrow{OB}=\overrightarrow{OA}\cdot\overrightarrow{OC}=\overrightarrow{OB}\cdot\overrightarrow{OC}$，则$O$是$\Delta ABC$的垂心；

证明：由于$\overrightarrow{OA}\cdot\overrightarrow{OB}=\overrightarrow{OA}\cdot\overrightarrow{OC}$，

则$\overrightarrow{OA}\cdot(\overrightarrow{OB}-\overrightarrow{OC})=0$，

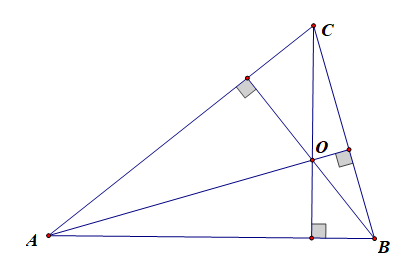
即$\overrightarrow{OA}\cdot\overrightarrow{CB}=0$，

则$OA\perp BC$，

同理可得$OB\perp AC$，$OC\perp AB$，

故$O$是$\Delta ABC$的垂心；

命题二、已知$O$为$\Delta ABC$所在平面内的一点，且$|\overrightarrow{OA}|^2+|\overrightarrow{BC}|^2=|\overrightarrow{OB}|^2+|\overrightarrow{CA}|^2=|\overrightarrow{OC}|^2+|\overrightarrow{AB}|^2$，则$O$是$\Delta ABC$的垂心；

四、三角形内心

内心：三角形的三个内角平分线的交点，内切圆的圆心

命题一、$O$为$\Delta ABC$的内心的充要条件是

$\overrightarrow{OA}\cdot(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}-\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|})$

$= \overrightarrow{OB}\cdot(\cfrac{\overrightarrow{BA}}{|\overrightarrow{BA}|}-\cfrac{\overrightarrow{BC}}{|\overrightarrow{BC}|})$

$=\overrightarrow{OC}\cdot(\cfrac{\overrightarrow{CA}}{|\overrightarrow{CA}|}-\cfrac{\overrightarrow{CB}}{|\overrightarrow{CB}|})=0$

证明：充分性，如图，向量$\overrightarrow{AB}、\overrightarrow{AC}$的单位向量分别是$\overrightarrow{AE}、\overrightarrow{AD}$，

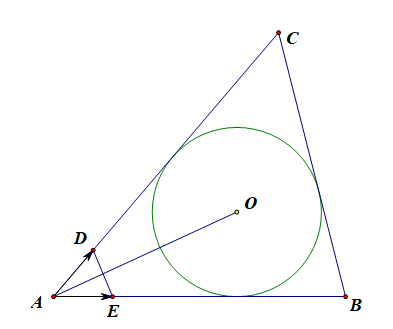
992978-20171017213753912-1982169177.png%20

则$\Delta ADE$为等腰三角形，

由$\overrightarrow{OA}\cdot (\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}-\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|})$

$=\overrightarrow{OA}\cdot (\overrightarrow{AE}-\overrightarrow{AD})$

$=\overrightarrow{OA}\cdot \overrightarrow{DE}=0$，

故$OA$为$\angle A$的平分线；

同理可得$OB、OC$为$\angle B、\angle C$的平分线；

故点$O$是$\Delta ABC$的内心。

必要性，由点$O$是$\Delta ABC$的内心，则可知$OA$为$\angle A$的平分线，

故容易知道$\overrightarrow{OA}\cdot \overrightarrow{DE}=0$，

即$\overrightarrow{OA}\cdot(\cfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}-\cfrac{\overrightarrow{AC}}{|\overrightarrow{AC}|})=0$，

同理可知$ \overrightarrow{OB}\cdot(\cfrac{\overrightarrow{BA}}{|\overrightarrow{BA}|}-\cfrac{\overrightarrow{BC}}{|\overrightarrow{BC}|})$

$=\overrightarrow{OC}\cdot(\cfrac{\overrightarrow{CA}}{|\overrightarrow{CA}|}-\cfrac{\overrightarrow{CB}}{|\overrightarrow{CB}|})=0$。

命题二、记$\overrightarrow{AB}、\overrightarrow{BC}、\overrightarrow{CA}$的单位向量为$\vec{e_1}$、$\vec{e_2}$、$\vec{e_3}$，则$O$为$\Delta ABC$的内心的充要条件是$\overrightarrow{OA}\cdot (\vec{e_1}+\vec{e_3})=\overrightarrow{OB}\cdot (\vec{e_1}+\vec{e_2})=\overrightarrow{OC}\cdot (\vec{e_2}+\vec{e_3})=\vec{0}$。